Correct Answer

verified
Correct Answer
verified
Short Answer
Determine where the function  is continuous.
is continuous.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the dimensions of a rectangular box of maximum volume such that the sum of the lengths of its 12 edges is 
A) ![]() ,
, ![]() ,
,![]()
B) 4, 8, 16
C) 32, ![]() , 16
, 16
D) ![]() ,
, ![]() ,
,![]()
E) 32, 32, 32
G) A) and E)
Correct Answer

verified
Correct Answer
verified
Short Answer
Find the first partial derivatives of the function 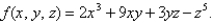
Correct Answer

verified
Correct Answer
verified
Short Answer
A cardboard box without a lid is to have a volume of 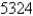 cm
cm  . Find the dimensions that minimize the amount of cardboard used.
. Find the dimensions that minimize the amount of cardboard used.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the Chain Rule to find 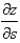 .
. 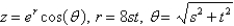
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) D) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use Lagrange multipliers to find the maximum value of the function subject to the given constraint. 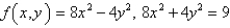
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the equation of the tangent plane to the given surface at the specified point. 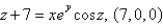
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) None of the above
Correct Answer

verified
Correct Answer
verified
Short Answer
Find and classify the relative extrema and saddle points of the function 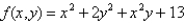 .
.
Correct Answer

verified
Relative m...View Answer
Show Answer
Correct Answer
verified
View Answer
Multiple Choice
Find the indicated partial derivative. 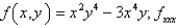
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) A) and B)
Correct Answer

verified
Correct Answer
verified
Short Answer
Use partial derivatives to find the implicit derivative 
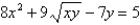
Correct Answer

verified
Correct Answer
verified
Short Answer
Find all the second partial derivatives. 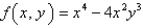
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find equations for the tangent plane and the normal line to the surface with equation  at the point
at the point 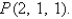
A) ![]() ,
, ![]()
B) ![]() ,
, ![]()
C) ![]() ,
, ![]()
D) ![]() ,
, ![]()
F) All of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Two contour maps are shown. One is for a function f whose graph is a cone. The other is for a function g whose graph is a paraboloid. Which is the contour map of a cone? 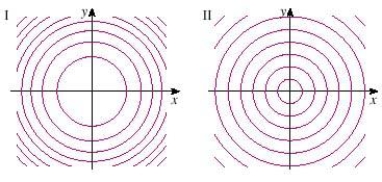
A) impossible to determine
B) II
C) I
E) All of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Evaluate the limit. 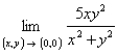
A) 0
B) the limit does not exist
C) ![]()
D) 1
E) 2
G) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use differentials to estimate the amount of metal in a closed cylindrical can that is 12 cm high and 8 cm in diameter if the metal in the top and bottom is 0.09 cm thick and the metal in the sides is 0.01 cm thick. (rounded to the nearest hundredth.)
A) 6.91 ![]()
B) 6.99 ![]()
C) ![]()
![]()
D) 8.34 ![]()
E) 6.7 ![]()
G) D) and E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the differential of the function 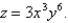
A) ![]()
B) ![]()
C) ![]()
D) ![]()
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find 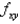 for the function
for the function 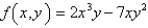 .
.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
G) A) and B)
Correct Answer

verified
Correct Answer
verified
Short Answer
Find 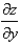 .
. 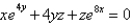
Correct Answer

verified
Correct Answer
verified
Short Answer
Find the limit. 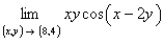
Correct Answer

verified
Correct Answer
verified
Showing 41 - 60 of 73
Related Exams